헤론의 공식: 삼각형 세변의 길이로

헤론 공식

헤론의 공식은 삼각형의 세 변의 길이가 주어졌을 때 삼각형의 넓이를 구하는 공식입니다. 이 공식은 수학자 헤론에 의해 발견되고 명명되었으며 헤로니우스 공식으로도 알려져 있습니다. 이 기사에서는 Heron의 공식의 기원, 적용 및 계산 방법을 살펴 보겠습니다.

삼각형의 면적 찾기: 문제 해결을 위한 간단한 공식

이등변삼각형의 넓이 공식: 기본 개념 및 응용

피타고라스의 정리: 직각삼각형의 변의 길이를 구하는 공식

직각 삼각형 면적 공식: 이해 및 사용

헤론 공식의 기원

헤론 공식은 오랫동안 사용되어 왔습니다. 예를 들어, 고대 이집트의 기록에는 이 공식을 사용하여 피라미드 밑면의 면적을 구하는 내용이 기록되어 있습니다. 그러나 Heron은 이 공식을 발견하고 확립했습니다. 헤론은 기하학과 삼각법을 공부한 그리스 수학자였습니다. 삼각형의 넓이를 구하는 다양한 방법을 연구하던 중, 그는 세 변의 길이만을 이용하여 삼각형의 넓이를 구하는 공식을 생각해 냈습니다. 그리스 수학자들은 이 공식을 사용하여 다양한 삼각형 문제를 풀었습니다.

헤론 공식의 응용

헤론의 공식은 삼각형 문제를 푸는 데 유용합니다. 예를 들어 세 변의 길이로 삼각형의 면적을 찾을 수 있습니다. 삼각형의 세 변 중 두 변의 길이와 그 사이의 각을 주면 삼각형의 한 변의 길이와 넓이도 구할 수 있습니다. 또한 헤론의 공식으로 다양한 삼각형 문제를 풀 수 있습니다.

헤론 공식의 계산 방법

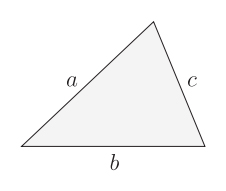
헤론의 공식은 다음과 같이 삼각형의 세 변의 길이 a, b 및 c를 사용하여 삼각형의 면적 S를 계산합니다.

s = (a + b + c) / 2
S = √(s(s-a)(s-b)(s-c))

여기서 s는 삼각형 둘레의 절반입니다. 위의 공식을 사용하여 삼각형의 면적을 찾을 수 있습니다. 그러나 이 식은 제곱근이므로 일반적으로 수동으로 계산하기 어렵습니다. 이를 해결하기 위해 계산기를 사용하거나 프로그래밍 언어를 사용하여 계산할 수 있습니다. 예를 들어, 다음은 Python에서 Heron 공식을 코드로 구현한 것입니다.

import math

def heron_formula(a, b, c):
    s = (a + b + c) / 2
    S = math.sqrt(s * (s - a) * (s - b) * (s - c))
    return S

위의 코드에서 수학 모듈의 sqrt 함수를 사용하여 제곱근을 계산하고 heron_formula 함수를 사용하여 삼각형의 면적을 계산할 수 있습니다. 이 기능을 사용하면 세 변의 길이를 사용하여 삼각형의 넓이를 쉽게 찾을 수 있습니다.

졸업 증서

헤론의 공식은 삼각형의 넓이를 구하는 데 유용한 오래된 공식입니다. 이번 글에서는 헤론 공식의 기원과 응용, 계산 방법에 대해 알아보았습니다.

헤론의 공식은 삼각형 문제를 푸는 데 중요한 역할을 하며 수학 문제를 푸는 데 유용합니다.