1. 나의 논리
(생각의 흐름)
– (카운트) 안의 숫자를 알파벳순으로 최하위로 출력
(고려 사항)
– 두 갈래로 나뉘는 경우 -> 숫자가 한쪽으로 치우치지 않아야 함
2. 논리
순열을 찾는 방법(DFS)
dy(n)(r) = combi(n-1, r-1) + combi(n-1, r)엔터티가 발견된 후 스택에 누적된 재귀를 호출하지 않고 즉시 종료되는 부울입니다.
flag = true;// 다른 재귀들을 없애기 위해서중복 값을 확인하는 방법
DFS(L+1, sum+(p(L)*b(L)));
ch(i)=0;
-마지막 숫자가 정확하다고 생각합니다.
– 하나하나 살펴보면 규칙이 나옵니다.
– 값은 N-1에서 값 조합의 내림차순으로 얻습니다.

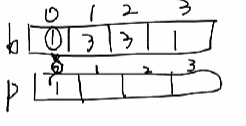
1) 첫 번째 배열: N개 값의 조합을 배열(0-N)에 저장
2) 두 번째 배열: 입력할 값
3) (동일한 수준) 합계 += 첫 번째 배열 * 두 번째 배열
4) 합계 = 마지막 값
5) 출력
public class Section8_8 {
static int() b, p, ch;
static int n, f;
boolean flag = false;
int ()() dy = new int(35)(35);
public int combi(int n, int r) { // 순열을 구해서 배열에 담음
if(dy(n)(r)>0) {
return dy(n)(r);
}
if(n==r||r==0) {
return 1;
}else {
return dy(n)(r) = combi(n-1, r-1) + combi(n-1, r);
}
}
public void DFS(int L, int sum) {
if(flag) return;
// 바로 리턴
if(L==n) {
if(sum==f) {
for(int x : p) {
System.out.println(x+" ");
flag = true;
}
}
}else {
for (int i = 1; i <= n; i++) { // 순열을 만드는 값 그 자체
if(ch(i)==0) { // 사용했니?
ch(i)=1;
p(L)=i;
DFS(L+1, sum+=(p(L)*b(L)));
ch(i)=0;
}
}
}
}
public static void main(String() args){
Section8_8 T = new Section8_8();
Scanner in=new Scanner(System.in);
n = in.nextInt(); ///4
f = in.nextInt();
b = new int(n); //순열을 담을 배열
p = new int(n); // 값을 담을 배열
ch = new int(n+1);
for (int i = 0; i < n; i++) {
b(i) = T.combi(n-1,i); // 순열
}
}![[파이썬] [백트래킹] 백준 7490 [파이썬] [백트래킹] 백준 7490](https://hurt.sicle.kr/wp-content/plugins/contextual-related-posts/default.png)